The Slope of a Line
Find the slope of the line given two points:
Consider two methods as alternatives for finding the slope: (without using the “slope-formulaâ€)
METHOD 1:
First, BUILD a TABLE starting with the given points in the middle of the table and find their
common differences, dx and dy, then we can use these differences to find the x-sequence
and y-sequence.
Since both columns must be arithmetic sequences, to get the next value below for the
x-sequence add dx , then add - dx to get the next value above to complete the x-sequence.
Similarly, to get the next value below for the y-sequence add dy, then add - dy to get the next
value above, and complete the y-sequence. (Always check both sequences.)
Recall that the slope is
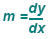and RECORD the value for m.
METHOD 2:
Plot BOTH points on a grid and move up/(down) and over to FIND values for dy and dx
and RECORD the value of m.
Now move using dy and dx to find the next point and continue up/over or down/over
to find several points. Label these points and put them in order in a table of sequences.
Example 1:
1. Given (2, -1) and (- 3, 2) plot the points and draw the line through the points.
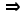 Put the points in the middle of the table and find the differences dx and dy.
See work below:
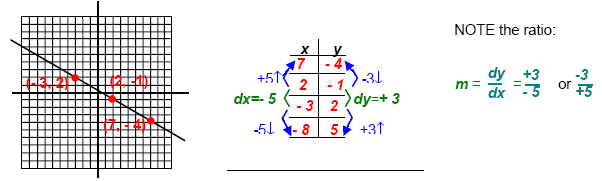
We found the slope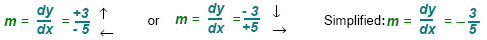
NOTE: A “neat†method for finding the slope (without using the “formulaâ€) is shown
below:
Ask “how far is it †from y1 to y2 in which direction (dy)
and “how far is it “ from x1 to x2 in which direction (dx).
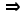Generally, it is better to place the points in the table or chart with x1 < x2
so that dx > 0.
These methods for finding the slope (without using the “formulaâ€) are illustrated in
the example below:
Example 2.
Given points: (3, 2), (5, -3) Find Dx and Dy directly from the table or the points.
Either order gives the same slope.
Example 3.
Given points: (3, 2), (6, - 2) Find dy and dx directly from the table or the points.
Either order gives the same slope.
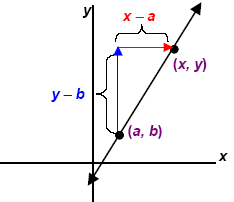
If we are given two points (a, b) and (x, y), and the slope m and we can use the slope- form
of the equation for the line:
 |
 |
 |
 |
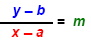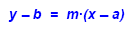Multiply each side by (x - a) |
| We can use this form to find the missing value
of two points (a, b), (c, d) if we know three of them.
|
Example 4.
Find x if the line through (3,3) and (x,9) has the slope of 2.
 |
 |
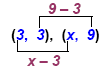
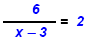Check: |
| 6 = 2 · (x - 3) |
Multiply each side by (x - 3) |
 |
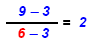| 6 = 2x - 6 |
Distributive property |
|
| 12 = 2x |
Addition property |
 |
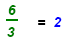| 6 = x |
Multiplication property |
|
|
