Adding and Subtracting Polynomials
Objective Learn how to add and subtract
polynomials.
This lesson is not difficult conceptually, but it is important
that you get sufficient practice in addition and subtraction of
polynomials.
Adding Polynomials
Let's begin with an example in order to see how to add
polynomials.
Example 1
Add x 3 + x + 1 and 3x 3 + x 2
+ 2x .
Solution
First, write the polynomials side by side.
( x 3 + x + 1 ) + ( 3x 3 + x 2
+ 2x )
The monomials x 3 and x each occur twice, so group
the terms together and combine them.
| x 3 + x + 1 + 3x 3
+ x 2 + 2x |
= ( x 3 + 3x 3 ) +
x 2 + ( x + 2x ) + 1 |
| |
= 4x 3 + x 2 + 3x +
1 |
This polynomial is simpler than the original two polynomials
written side by side.
Like Terms
To be explicit about the steps taken to add polynomials, let's
talk a little bit about like terms.
Definition of Like Terms
When we are given two polynomials, we say the monomials in the
polynomials are like terms if they contain exactly the same
number of occurrences of each variable.
Example 2
Name the like terms in x 4 + 4x 3 + 6x
2 + 4 x + 1 and x 3 + x 2 + 1.
Solution
There are several pairs of like terms, shown in the diagram
below.
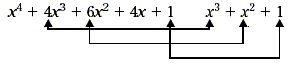
The pairs of like terms are connected by arrows. So, the like
terms are 4x 3 and x 3 , 6x 2
and x 2 , 1 and 1.
Example 3
Name the like terms in ab + 2a + 2b and ab - a + 1.
Solution
In this case, there are two pairs of like terms, ab and ab ,
2a and -a , shown in the diagram below.
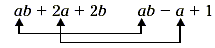
Whenever there are like terms, collect them and add them
together to get a single term. In Example 2, add 4x 3
and x 3 together to get 5x 3 . In the same
way, add 6x 2 and x 2 together to get 7x
2 , and finally, 1 + 1 = 2.
When we do this, we get a simpler polynomial.
( x 4 + 4x 3 + 6x 2 + 4 x + 1
) + ( x 3 + x 2 + 1 ) = x 4 + 5x
3 + 7x 2 + 4x + 2
In Example 3, collect the ab and a terms to get
( ab + 2a + 2b ) + ( ab - a + 1) = 2ab + a + 2b + 1.
Key Idea
Sums of polynomials can be simplified by adding together like
terms. In the same way, differences of polynomials can be
simplified by collecting together all pairs of like terms.
Subtracting Polynomials
Example 4
Simplify ( x 3 - 3x 2 + 3 x - 1) - ( x
2 + 2x + 1).
Solution
First write this as an addition expression by adding the
additive inverse.
( x 3 - 3x 2 + 3 x - 1) - ( x 2
+ 2x + 1) = ( x 3 - 3x 2 + 3 x - 1) + ( -x
2 - 2x - 1)
To simplify the difference, collect all pairs of like terms.
These are shown in the diagram below.
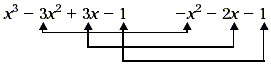
Collect the terms to get the following polynomial.
x 3 + ( - 3 - 1) x 2 + (3 - 2) x + ( - 1
- 1) = x 3 - 4x 2 + x - 2
There is another method of adding and subtracting polynomials
that is similar to adding and subtracting numbers. Write the
polynomials one over the other, with like terms lined up in
columns. To find the difference, either subtract the coefficients
in each of the columns, or add the additive inverse.
Example 5
Subtract 4x 3 + 5x 2 + 6x + 7 and 2x
3 + 3x + 4.
Solution
Write the polynomials with the like terms in columns.
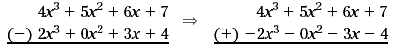
Notice that a zero coefficient is added for each missing term.
Now add the coefficients in each column.
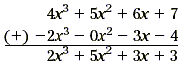
|