Dividing Monomials
After studying this lesson, you will be able to:
- Divide monomials.
- Simplify expressions with negative exponents.
Dividing Powers with the Same Base: The base
stays the same; Subtract the exponents
After subtracting the exponents, you will put the remaining
exponent where the largest exponent was to begin with. For
example, if you have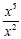 
which is a division problem, we will subtract the exponents 5 -2
which gives us 3. We will be left with x 3 . We leave
this in the numerator, since the largest exponent was in the
numerator to begin with.
Example 1
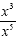
We are dividing powers with the same base (x). So, we keep the
base and we subtract the exponents. We will have x to the 2
nd power and we put that in the denominator since the
larger exponent was in the denominator to begin with.
The answer will be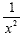 
. We have to put a 1 in the numerator to hold the place. You
can't leave the numerator without anything there.
Example 2
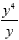
We are dividing powers with the same base (y). So, we keep the
base and we subtract the exponents. We will have y to the 3
rd power and we put that in the numerator since the larger
exponent was in the numerator to begin with.
The answer will be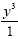 
or y 3 . We don't have to put a 1 in the denominator.
Example 3
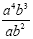
We are dividing powers with the same base (a and b). So, we
keep the bases and we subtract the exponents
The answer will be a 3 b.
Now we're going to work with expressions that have
coefficients. Remember that coefficients are the
numbers in front of the variables. When dividing powers with the
same base, we subtract the exponents. We also divide or reduce
the coefficients.
Example 4
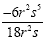
The coefficients are -6 and 18 so we either divide or reduce
those. In the case, we need to reduce the coefficients. The
exponents of r are 2 and 2 so we subtract those. The exponents of
s are 5 and 1 so we subtract those.
This will give us an answer of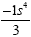 
s because -6 and 18 reduces to -1 and 3. When we subtract the
exponents of r we find that they cancel each other out. When we
subtract the exponents of s, we are left with s 4 . We
put that in the numerator since the larger exponent was in the
numerator to begin with.
Example 5
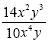
The coefficients are 14 and 10 so we either divide or reduce
those. In the case, we need to reduce the coefficients. 14 and 10
will reduce to 7 and 5. The exponents of x are 2 and 4 so we
subtract those. The exponents of y are 1 and 1 so we subtract
those. The x 2 will go in the denominator and the y
2 will go in the numerator.
This will give us an answer of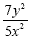 
|
