Rationalizing the Denominator
Example 1
Simplify:
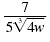
| Solution |
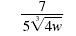 |
| Factor the radicand. |
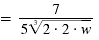 |
The radical in the denominator is a cube root. To rationalize the
denominator, we want to make the radicand a perfect cube.
- 2 occurs twice as a factor. To make a perfect cube, we multiply by 2.
- w occurs once as a factor. To make a perfect cube, we multiply by w2.
We multiply by 1 written in the form
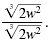 |
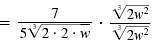 |
| Multiply the numerators and multiply
the denominators.
|
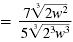 |
| Simplify the denominator. |
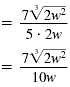 |
| So, |
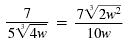 |
Suppose we have a radical expression such as
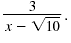
Recall that when we multiply conjugates, the result is always a rational
number.
Therefore, to eliminate the radical in the denominator of the expression,
we multiply the numerator and denominator by
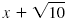 , the conjugate
of the denominator. , the conjugate
of the denominator.
Example 2
Simplify:
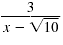
| Solution |
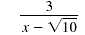 |
To rationalize the denominator
we multiply the numerator
and denominator by
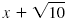 , the conjugate of x , the conjugate of x
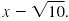 |
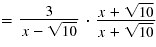 |
| Multiply the numerators and
multiply the denominators.
|
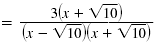 |
| Remove the parentheses. |
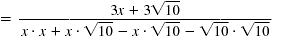 |
| Simplify the denominator.
The two middle terms add
to zero. |
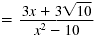 |
| So, |
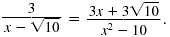 |
|