Exponential Functions

Laws of Exponents

If s, t, a and b are real numbers, with a > 0 and b > 0, then:

1) a^s · a^t = a^{s + t}

2) (a^s)^t = a^st

3) (ab)^s = a^s · b^s

4)

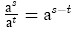
5)

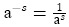
6)

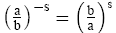
7) 1^s = 0

8) a⁰ = 1

Exponential Functions

Definition: If b is a positive real number, b ≠ 1, the exponential function with base b is f(x) = b^x , for every real number x.

Examples:

f(x) = 2x	f(x) = 3x

Properties of Exponential Functions of the Form f(x) = b^x

1. b^x > 0 for all numbers, x; so, the range of these functions is (0, ∞).

2. Their domains will be (-∞, ∞).

3. All will have y-intercepts at (0,1) and no x-intercepts.

4. The x-axis is a horizontal asymptote.

5. If b > 1, f(x) = b^x is an increasing function. If 0 < b < 1, f(x) = b^x is a decreasing function.

6. They are all one-to-one.

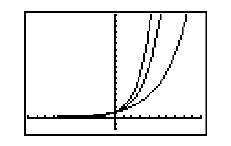
Here is a graph with f(x) = 2^x , f(x) = 3^x and f(x) = 4^x all on the same screen. Can you tell which is which?

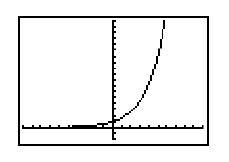
The Natural Exponential Function: f(x) = e^x

e is a special number in mathematics, and is approximately 2.7182818. Since e > 1, the graph of the exponential function is shaped like the graph of f(x) = 2^x. It is an increasing function. e^x > 0 for all numbers x. Here is the graph of f(x) = e^x:

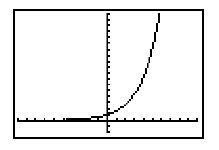
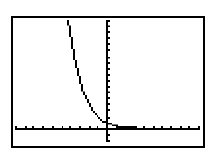
Exponential Growth Functions Any function of the form y = a(bx), b > 1, a > 0, is an exponential growth function. Its graph will increase on its entire domain.	Exponential Decay Function Any function of the form y = a(bx), b > 1, a > 0, or y = a(c ), 0 c 1, a 0, is an exponential decay function, and will decrease on its domain.