Mixed Numbers and Improper Fractions
On many jobs if you work overtime, the rate of pay increases
to one-and-a-half times the regular rate. A number such as 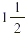 with a whole number part and a proper fraction part,
is called a mixed number. A mixed number can also be expressed as
an improper fraction, that is, a fraction whose numerator is
larger than or equal to its denominator. The number with a whole number part and a proper fraction part,
is called a mixed number. A mixed number can also be expressed as
an improper fraction, that is, a fraction whose numerator is
larger than or equal to its denominator. The number 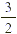 is an example of an improper fraction. is an example of an improper fraction.
Explain why a fraction whose numerator is larger than or equal
to its denominator must have a value greater than or equal to 1.
Diagrams help us understand that mixed numbers and improper
fractions are different forms of the same numbers, as Example 1
illustrates.
EXAMPLE 1
Draw diagrams to show that 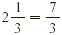 . .
Solution
First, represent the mixed number and the improper fraction in
diagrams.
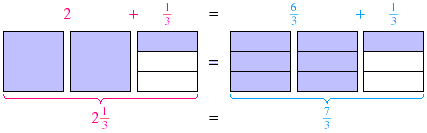
Both diagrams represent 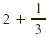 so the numbers so the numbers 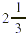 and and 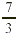 must be equal. must be equal.
In Example 1 each unit (or square) corresponds to one whole,
which is also three-thirds. That is why the total number of
thirds in 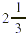 is (2 is (2 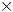 3) + 1, or 7. The number of wholes in 3) + 1, or 7. The number of wholes in 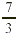 is 2 wholes, with is 2 wholes, with 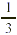 of a whole left over. We can generalize these
observations into two rules. of a whole left over. We can generalize these
observations into two rules.
To Change a Mixed Number to an Improper Fraction
- multiply the denominator of the fraction by the whole
number part of the mixed number,
- add the numerator of the fraction to this product, and
- write this sum over the original denominator to form the
improper fraction.
EXAMPLE 2
Write each of the following mixed numbers as an improper
fraction.
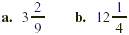
Solution
a. We first multiply the denominator 9 by the
whole number 3, getting 27. We next add the numerator 2. We then
write the sum 29 over the original denominator to get 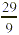 . .
b.
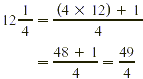
To Change an Improper Fraction to a Mixed Number
- divide the numerator by the denominator, and
- if there is a remainder, write it over the denominator.
EXAMPLE 2
Write each improper fraction as a mixed or whole number.
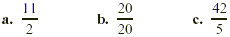
Solution
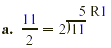 Divide the numerator by the denominator. Divide the numerator by the denominator.
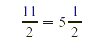 Write the remainder over the denominator. Write the remainder over the denominator.
In other words, 5 R1 means that in 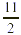 there are 5 wholes with there are 5 wholes with 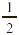 of a whole left over. of a whole left over.
Changing an improper fraction to a mixed number is important
when we are dividing whole numbers: It allows us to express any
remainder as a fraction. Previously, we would have said that the
problems 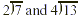 both have the answer 3 R1. But by
interpreting these problems as improper fractions, we see that
their answers are different. both have the answer 3 R1. But by
interpreting these problems as improper fractions, we see that
their answers are different.
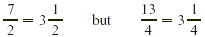
When a number is expressed as a mixed number, we know its size
more readily than when it is expressed as an improper fraction.
For instance, consider the mixed number 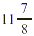 . We immediately see that it is larger
than 11 and smaller than 12 (that is, between 11 and 12). We
could not reach this conclusion so easily if we were to examine
only . We immediately see that it is larger
than 11 and smaller than 12 (that is, between 11 and 12). We
could not reach this conclusion so easily if we were to examine
only 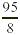 its improper form. However, there are
situations—when we multiply or divide fractions—in
which the use of improper fractions is preferable. its improper form. However, there are
situations—when we multiply or divide fractions—in
which the use of improper fractions is preferable.
|