Identifying Prime and Composite Numbers
Now let’s discuss the difference between prime numbers
and composite numbers.
Definitions
- A prime number is a whole number that
has exactly two factors: itself and 1.
- A composite number is a whole number
that has more than two factors.
Note that the numbers 0 and 1 are neither prime nor composite.
But every whole number greater than 1 is either prime or
composite, depending on its factors.
For instance, 5 is prime because its only factors are 1 and 5.
But 8 is composite because it has more than two factors (it has
four factors: 1, 2, 4, and 8).
Let’s practice distinguishing between primes and
composites.
EXAMPLE 1
Indicate whether each number is prime or composite.
a. 2
b. 78
c. 51
d. 19
e. 31
Solution
a. The only factors of 2 are 1 and 2.
Therefore 2 is prime.
b. Because 78 is even, it is divisible by 2.
Having 2 as an “extra” factor—in addition to 1 and
78—means that 78 is composite. Do you see why all even
numbers, except for 2, are composite?
c. Using the divisibility test for 3, we see
that 51 is divisible by 3 because the sum of the digits 5 and 1
is divisible by 3. Because 51 has more than two factors, it is
composite.
d. The only factors of 19 are itself and 1.
Therefore 19 is prime.
e. Because 31 has no factors other than
itself and 1, it is prime.
Finding the Prime Factorization of a Number
Every composite number can be written as the product of prime
factors. This product is called its prime factorization. For
instance, the prime factorization of 12 is 2 · 2 · 3.
Definition
The prime factorization of a whole number is
the number written as the productof its prime factors.
There is exactly one prime factorization for any composite
number. This statementis called the fundamental theorem
of arithmetic.
Being able to find the prime factorization of a number is an
important skill to have for working with fractions, as we show
later in this chapter. A good way to find the prime factorization
of a number is by making a factor tree, as illustrated in Example
6.
EXAMPLE 2
Write the prime factorization of 72.
Solution
We start building a factor tree for 72 by dividing 72 by the
smallest prime, 2.
Because 72 is 2 · 36, we write both 2 and 36 underneath the
72. Then we circle the 2 because it is prime.
Next we divide 36 by 2, writing both 2 and 18, and circling 2
because it is prime. Below the 18, we write 2 and 9, again
circling the 2. Because 9 is not divisible by 2, we divide it by
the next smallest prime, 3. We continue this process until all
the factors in the bottom row are prime.
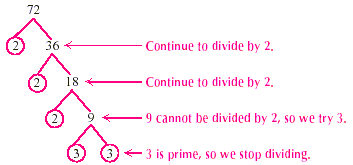
The prime factorization of 72 is the product of the circled
factors.
72 = 2 × 2 × 2 × 3 × 3
We can also write this prime factorization as 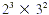 . .
An alternative approach is the following.
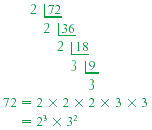
EXAMPLE 3
Express 60 as the product of prime factors.
Solution
The factor tree method for 60 is as shown.
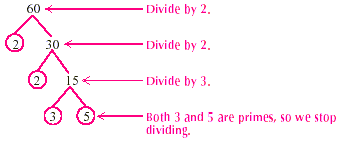
The prime factorization of 60 is 2 × 2 × 3 × 5, or 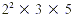 . .
|