Conjugates
In the previous example, we multiplied two radical expressions,
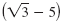 and and
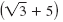 . .
You may have been surprised that the result -22, does not contain a
radical.
Let’s recall why that is so.
We used the FOIL method to multiply:

Let’s look again at the original two radical expressions.
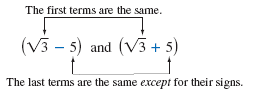
Such binomial radical expressions are called conjugates.
Here are some other examples of conjugates:
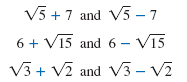
When we multiply two conjugate radical expressions, the result is a
rational number. For this reason, conjugates are used to simplify certain
types of radical expressions.
Example 1
Multiply
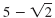 by its conjugate. by its conjugate.
Solution
The conjugate of
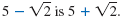 |
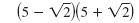 |
| Use the FOIL method.
|
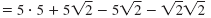 |
| Multiply.
|
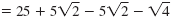 |
| The two middle terms are
opposites and add to zero. |
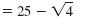 |
Simplify
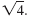 |
= 25 - 2 |
| Subtract. |
= 23 |
|