Solving One-Step Equations Using Models
Objective Learn how to solve linear equations
using models.
While modeling the solution steps for an equation, be sure to
understand the algebra involved in each step.
Representing Equations with Models
Equations involving a single variable and integers can often
be represented using models. The variable is represented by a
single object and counters are used to represent the integers.
The counters are shown here as either gray circles for a positive
integer or black circles for a negative integer. To represent
equations here using the models, we draw the same number of cups
as the number of times the variable occurs, and place the
appropriate number of counters on each side of the equal sign to
model the integers occurring in the equation.
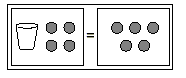
Example 1
x + 4 = 5
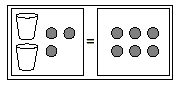
Example 2
2x + 3 = 6
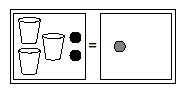
Example 3
3x - 2 = 1
Solving One-Step Equations Using Models
Once the equations have been modeled, they can be manipulated
by adding and removing gray or black counters to either side of
the model. When there are both gray and black counters on one
side, the counters can be paired up and removed. The removal of
these pairs corresponds the fact that 1 + (-1) = 0, since a gray
counter represents +1 and a black counter represents -1.
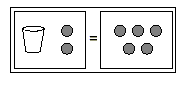
Example 4
Solve x + 2 = 5 for x .
Solution
First we model the equation.
Then we remove the same number of counters from each side
until the cup is alone. It is critical that the same number of
counters are removed from each side. To get the cup alone, we
need to remove 2 gray counters from each side.
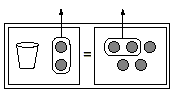
This manipulation corresponds to subtracting the number 2 from
each side of the equation.
After removing counters (2 from each side), the model now
looks like this.
The model above tells us that x = 3.
We can verify that this value of x is the correct solution by
replacing x with it in the original equation: 3 + 2 = 5. This is
correct.
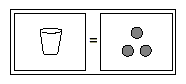
Example 5
Use a model to solve x - 4 = 2.
Solution
This equation involves subtraction on one side. Subtraction of
an integer is the same as the addition of the opposite integer.
Therefore, the equation x - 4 = 2 can be rewritten as the
equation x + ( - 4) = 2. The model for this equation is given
below.
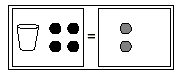
To get the cup alone in the model, we need to remove the 4
black counters that are on the left side of the equation. But
since there are no black counters on the other side, we cannot
use the technique shown in Example 4. In order to be able to
remove the black counters, we need to add 4 gray counters to each
side. As long as we add the same number and color of counters to
each side, the new model will be equivalent to the original
model. The model with 4 gray counters added to each side is shown
below.
Now we can remove the four pairs of gray and black counters
from the left side of the model. We are left with this model.
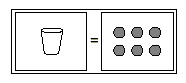
This model represents the equation x = 6. Replacing x in the
original equation with 6 gives the true number sentence 6 - 4 =
2, so the solution is correct.
The following equation requires the use of more than one cup
in the model. The solution of the equation is the value of x ,
that is, the value of just one x.
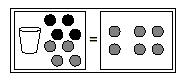
Example 6
Solve 2x = 6.
Solution
Model the equation.
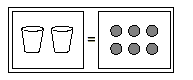
Thinking of the equation as x + x = 6 is helpful at this step.
There are two x s modeled on the left side of the figure, and
that we can separate the counters on the right side into two
groups of 3 counters each. We can then assign one group of 3
counters to each cup.
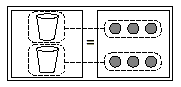
Since we are interested only in how many counters go with one
x, we can focus on just one of the two parts of the previous
model. The model at the bottom of the previous page shows that x
= 3.
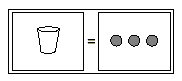
This result can be verified by substituting 3 for x in the
original equation.
The process in this example corresponds to dividing each side
of the equation by 2. This process is not as clear from the
models as it is when we add or remove counters from each side.
|