
	Home
	Systems of Equations
	Adding and Subtracting Rational Expressions with Different Denominators
	Graphing Linear Equations
	Raising an Exponential Expression to a Power
	Horizontal Line Test
	Quadratic Equations
	Mixed Numbers and Improper Fractions
	Solving Quadratic Equations by Completing the Square
	Solving Exponential Equations
	Adding and Subtracting Polynomials
	Factorizing simple expressions
	Identifying Prime and Composite Numbers
	Solving Linear Systems of Equations by Graphing
	Complex Conjugates
	Graphing Compound Inequalities
	Simplified Form of a Square Root
	Solving Quadratic Equations Using the Square Root Property
	Multiplication Property of Radicals
	Determining if a Function has an Inverse
	Scientific Notation
	Degree of a Polynomial
	Factoring Polynomials by Grouping
	Solving Linear Systems of Equations
	Exponential Functions
	Factoring Trinomials by Grouping
	The Slope of a Line
	Simplifying Complex Fractions That Contain Addition or Subtraction
	Solving Absolute Value Equations
	Solving Right Triangles
	Solving Rational Inequalities with a Sign Graph
	Domain and Range of a Function
	Multiplying Polynomials
	Slope of a Line
	Inequalities
	Multiplying Rational Expressions
	Percent of Change
	Equations Involving Fractions or Decimals
	Simplifying Expressions Containing only Monomials
	Solving Inequalities
	Quadratic Equations with Imaginary Solutions
	Reducing Fractions to Lowest Terms
	Prime and Composite Numbers
	Dividing with Exponents
	Dividing Rational Expressions
	Equivalent Fractions
	Graphing Quadratic Functions
	Polynomials
	Linear Equations and Inequalities in One Variable
	Notes on the Difference of 2 Squares
	Solving Absolute Value Inequalities
	Solving Quadratic Equations
	Factoring Polynomials Completely
	Using Slopes to Graph Lines
	Fractions, Decimals and Percents
	Solving Systems of Equations by Substitution
	Quotient Rule for Radicals
	Prime Polynomials
	Solving Nonlinear Equations by Substitution
	Simplifying Radical Expressions Containing One Term
	Factoring a Sum or Difference of Two Cubes
	Finding the Least Common Denominator of Rational Expressions
	Conjugates
	Multiplying Rational Expressions
	Expansion of a Product of Binomials
	Solving Equations
	Exponential Growth
	Factoring by Grouping
	Solving One-Step Equations Using Models
	Solving Quadratic Equations by Factoring
	Adding and Subtracting Polynomials
	Rationalizing the Denominator
	Rounding Off
	The Distributive Property
	What is a Quadratic Equation
	Laws of Exponents and Multiplying Monomials
	The Slope of a Line
	Factoring Trinomials by Grouping
	Multiplying and Dividing Rational Expressions
	Solving Linear Inequalities
	Multiplication Property of Exponents
	Multiplying and Dividing Fractions 3
	Formulas
	Dividing Monomials
	Multiplying Polynomials
	Adding and Subtracting Functions
	Dividing Polynomials
	Absolute Value and Distance
	Multiplication and Division with Mixed Numbers
	Factoring a Polynomial by Finding the GCF
	Roots
	Adding and Subtracting Polynomials
	The Rectangular Coordinate System
	Polar Form of a Complex Number
	Exponents and Order of Operations
	Graphing Horizontal and Vertical Lines
	Invariants Under Rotation
	The Addition Method
	Solving Linear Inequalities in One Variable
	The Pythagorean Theorem

Try the Free Math Solver or Scroll down to Tutorials!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Degree of a Polynomial

The degree of a term of a polynomial is the sum of the exponents of the variables in that term.

For example, consider this trinomial:		6x³y² + xy² + 3⁵x⁴.
The degree of the first term is 5.	degree	6x³y² = 3 + 2 = 5
The degree of the second term is 3.	degree	xy² = x¹y² = 1 + 2 = 3
The degree of the last term is 4. In 35, the exponent does not contribute to the degree because the base, 3, is not a variable.	degree	3⁵x⁴ = 4
The degree of a polynomial is equal to the degree of the term with the highest degree.
In this polynomial, the term with the highest degree has degree 5. So this polynomial has degree 5.	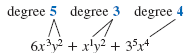The polynomial has degree 5.