Simplifying Radical Expressions Containing One
Term
Here is what we mean by the simplified form of a radical expression that
contains one term.
Definition — Simplified Form of a Radical Expression That Contains One Term
A radical expression that contains one term is in simplified form
when:
• For
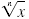 there are no factors of x, other than 1, that are perfect nth
powers.
• There are no fractions under the radical symbol.
• There are no radicals in the denominator of an expression.
| Here are some examples: |
Not simplified |
| • For
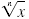there are no factors of x, other
than 1, that are perfect nth powers. |
 |
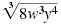| • There are no fractions under the radical symbol. |
 |
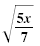| • There are no radicals in the denominator of a fraction. |
 |
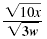Example
Simplify:
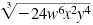
Solution
| This radical is a cube root. It is not in simplified form because the radicand
has some factors that are perfect cubes. To begin, we identify those factors. |
 |
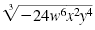| Factor the radicand. Use perfect cube factors when possible. |
 |
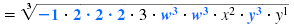| Write as a product of radicals. Place each perfect cube under its own
radical symbol. You can leave the “noncube†factors under the same
radical symbol. |
 |
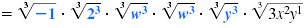| Simplifying the cube root of each perfect cube. |
 |
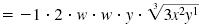| Multiply the factors outside the radical symbol. |
 |
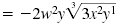| So, |
 |
|
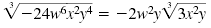