Polynomials
Recall that a monomial is a number, a variable, or a product
of numbers andvariables. A polynomial is a
monomial or a sum of monomials. The exponents of the variables of
a polynomial must be positive. A binomial isthe
sum of two monomials, and a trinomial is the sum
of three monomials. The degree of a monomial is
the sum of the exponents of its variables. To find the degree of
a polynomial, you must find the degree of each term. The greatest
degree of any term is the degree of the polynomial. The terms of
a polynomial are usually arranged so that the powers of one
variable are in ascending or descending order.
Examples
Consider the expression 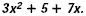 . .
A Is the expression a polynomial and if so is
it a monomial, binomial, or trinomial?
The expression is the sum of three monomials, therefore it is
a polynomial. Since there are three monomials, the polynomial is
a trinomial.
B What is the degree of the polynomial?
The degree of 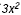 is 2, the degree of 5 is 0, and the
degree of 7x is 1. The greatest degree is 2, so the degree of the
polynomial is 2. is 2, the degree of 5 is 0, and the
degree of 7x is 1. The greatest degree is 2, so the degree of the
polynomial is 2.
C Arrange the terms of the polynomial so
thatthe powers of x are in descending order.
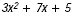
Adding and Subtracting Polynomials
To add polynomials, you can group like terms and then find
their sum, or youcan write them in column form and then add. To
subtract a polynomial, add its additive inverse, which is the
opposite of each term in the polynomial.
Examples
Find each sum or difference.
A 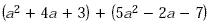
Arrange like terms in column form and add. Follow the rules
for adding signed numbers.
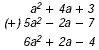
B (12x + 7y ) - (- x + 2y )
Find the additive inverse of - x + 2y. Then group the like
terms and add. The additive inverse of - x + 2y is x - 2y.
(12x + 7y ) - (- x + 2y )
= (12x + 7y ) + (+ x - 2y )
= (12x + x) + (7y - 2y)
= 13x + 5y
Multiplying a Polynomial by a Monomial
Use the distributive property to multiply a polynomial by a
monomial. Youmay find it easier to multiply a polynomial by a
monomial if you combine alllike terms in the polynomial before
you multiply.
Examples
Find 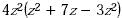
Solution
Combine like terms in the polynomial and then multiply using
the distributive property.
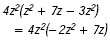
Multiplying Polynomials
Use the distributive property to multiply polynomials. If you
are multiplying two binomials, you can use a shortcut called the
FOIL method.
To multiply two binomials, find the sum of the products of
| FOIL Method for Multiplying Two
Binomials |
F the First terms O the Outer terms
I the Inner terms
L the Last terms
|
Example
Find (2x + 3)(4x - 1).
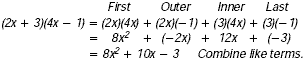
|