Solving Nonlinear Equations by Substitution
Example
Solve for w: (w2 - 5w)2 - 5(w2 - 5w) = 14
| Solution Step 1 Write the equation in quadratic form.
Subtract 14 from both sides.
Step 2 Use an appropriate “u†substitution.
Substitute u for w2 - 5w.
Step 3 Solve the resulting equation.
|
(w2 - 5w)2 - 5(w2
- 5w)
(w2 - 5w)2 - 5(w2 - 5w)1 -
14
u2 - 5u - 14
|
= 14
= 0
= 0
|
|
Factor the new equation.
Use the Zero Product Property.
Solve each equation for u.
Step 4 Substitute the original
expression for u.
Step 5 Solve for the original variable.
|
(u - 7)(u + 2)
u - 7 = 0 or u + 2
u = 7 or u
w2 - 5w = 7 or w2 - 5w |
= 0
= 0
= -2
= -2 |
Write each equation in standard form. Then, use
the quadratic formula to solve each equation.
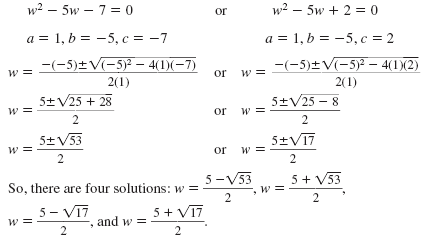
The equation (w2 - 5w)2 - 5(w2 - 5w) = 14 written in standard form is
(w2 - 5w)2 - 5(w2 - 5w) - 14 = 0. The graph of the corresponding
function, f(w) = (w2 - 5w)2 - 5(w2 - 5w) - 14 is shown.
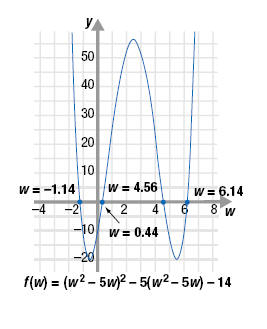
The graph crosses the w-axis at four locations:
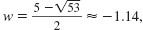
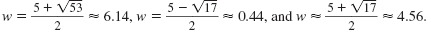
|