Solving Quadratic Equations by Factoring
Example 1
Solve by factoring: x2 - 14 = -5x
Solution
| Step 1 Write the equation in the form ax2
+ bx + c = 0 Add 5x to both sides.
Step 2 Factor the polynomial.
The coefficient of x2 is 1, so find two
numbers whose product is -14 and
whose sum is 5.
|
x2 + 5x - 14 |
= 0 |
| These numbers are -2 and 7.
Step 3 Use the Zero Product Property.
Step 4 Solve the resulting equations.
Step 5 Check each answer.
We leave the check to you. |
(x - 2)(x + 7) x - 2 = 0
x = 2 |
= 0 or x + 7 = 0
or x = -7 |
So, the two solutions of x2 - 14 = -5x are x = 2 and x = -7.Example 2
Solve by factoring: 7x + 6x2 = 20
Solution
| Step 1 Write the equation in the form ax2
+ bx + c = 0 Subtact 20 from both sides.
Step 2 Factor the polynomial.
The coefficient of x2 is not 1, so find two numbers
whose product is ac and whose sum is b.
ac = 6(-20) = -120 , b = 7
The two numbers are -8 and 15. |
6x2 + 7x - 20 |
= 0 |
| Rewrite the middle term,
7x, as -8x + 15x.
Factor 2x from the first pair
of terms.
Factor 5 from the second pair
of terms.
Factor out the common
binomial factor, 3x - 4. Step 3 Use the Zero Product Property.
Step 4 Solve the resulting equations.
Step 5 Check each answer.
We leave the check to you. |
6x2 - 8x + 15x
- 20
2x(3x - 4) + 5(3x - 4)
(3x - 4)(2x + 5) 3x - 4 = 0 or 2x + 5
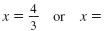 |
= 0
= 0
= 0 = 0
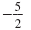 |
So, the two solutions of 7x + 6x2 = 20 are
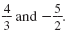
|