Quadratic Equations
Using the Discriminant to predict the roots of a quadratic
equation
The discriminant of a quadratic equation is the value under
the square root sign in the quadratic formula.
Remember the quadratic formula for an equation in the form ax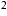 + bx + c = 0 is:
+ bx + c = 0 is:
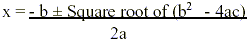
From this formula the discriminant is: b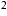 - 4ac
- 4ac
When you evaluate the discriminant for a quadratic equation,
if the result is:
| positive |
You will have 2 different real solutions
to the equation |
| |
If this number is a perfect square
number, there will be 2 different rational answers. If
this number is a not perfect square number, there will be
2 different irrational answers. |
| zero |
You will have 1 real, rational solution
to the equation - that is, there will be a repeated
answer |
| negative |
You will have no real solutions to the
equation (only imaginary answers) |
Examples:
Use the discriminant to predict the roots of the following
equations:
1. x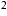 + 7x + 12 = 0 + 7x + 12 = 0 |
a = 1 |
b = 7 |
c = 12 |
b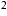 - 4ac = 7 - 4ac = 7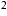 - 4(1)(12) = 49 - 48 = 1 - 4(1)(12) = 49 - 48 = 1 |
Since the result is positive, there should be 2 different real
solutions.
In fact, there will be 2 different rational solutions because
1 is a perfect square number.
(Perfect square numbers are: 1, 4, 9, 16, 25, 36, 49, 64, 81,
100, 121, 144, etc)
2. x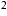 + 7x + 3 = 0 + 7x + 3 = 0 |
a = 1 |
b = 7 |
c = 3 |
b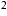 - 4ac = 7 - 4ac = 7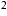 - 4(1)(3) = 49 - 12 = 37 - 4(1)(3) = 49 - 12 = 37 |
Since the result is positive, there should be 2 different real
solutions.
In fact, there will be 2 different irrational solutions
because 37 is not a perfect square number.
3. x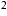 + 4x + 4 = 0 + 4x + 4 = 0 |
a = 1 |
b = 4 |
c = 4 |
b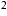 - 4ac = 4 - 4ac = 4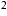 - 4(1)(4) = 16 - 16 = 0 - 4(1)(4) = 16 - 16 = 0 |
Since the result is zero, there should be only one real,
rational solution
4. x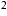 - x + 4 = 0 - x + 4 = 0 |
a = 1 |
b = -1 |
c = 4 |
b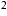 - 4ac = (-1) - 4ac = (-1)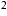 - 4(1)(4) = 1 - 16 = -15 - 4(1)(4) = 1 - 16 = -15 |
Since the result is negative, there should be no real
solutions.
|