Simplifying Expressions Containing only Monomials
We call monomials to those algebraic
expressions consisting of a single term (although this term may
contain subexpressions which do contain more than one term). In
the following excercises we concentrate on the simplification of
simple products, quotients, and powers – in fact, we are
reviewing and illustrating the laws of exponents, but using
algebraic expressions rather than simple numerical expressions.
We could say that "the rules" for combining powers
are the following:
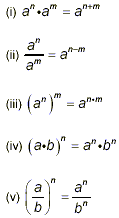
Usually simplification involves combining rules (iv) and (v)
with one or more of rules (i), (ii), or (iii). When division is
involved, rule (ii) brings in something like cancelling common
factors between the numerator and the denominator of a fraction.
Remember that multiplication with simple numbers or symbols
representing simple numbers is commutative
– the order of the factors doesn’t matter:
a · b = b · a
Example 1:
Simplify 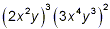
solution:
Property (iv) can be applied to products of more than two
factors. All we need to remember to do is to apply the power
outside the brackets to every factor inside the bracket. So
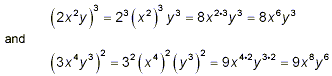
Thus, we get
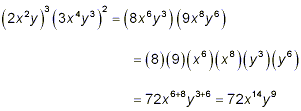
Rule (i) can be used with a product of more than two factors
as well.
Example 2:
Simplify 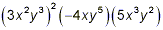
solution:
Separate all products into factors involving either a number
or a power of a single symbol:
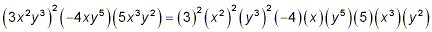
Now, rule (i) applies only when the powers being multiplied
are powers of the same number or symbol – represented by the
symbol ‘a’ in the statement of the rule at the
beginning of this document. So, to position the factors in our
expression for a potential simplification using rule (i), we
rearrange individual factors to get matching symbols in sequence:
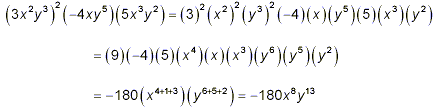
Note that in the above work, we used the fact that x = x
1 . Thus, for example
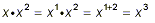
is a product of two factors of x. So, multiplying x 2
by x means the result has an additional factor of x, or three
factors of x, hence needs to be written as x 3 . This
is what results when we replace x by x 1 and then
apply rule (i) for multiplying two powers together. Take care
when the expression being simplified has a leading minus sign.
Example 3:
Simplify 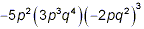
solution:
The easiest way to take correct account of the leading minus
sign is to keep it attached to the 5 in this case. Then,
separating powers of each symbol and rearranging the order of the
factors appropriately as we did in the previous example, we get
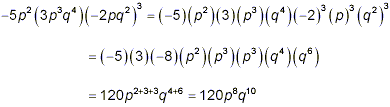
|