Solving Right Triangles
Example 1
Solve the right triangle sketched below.
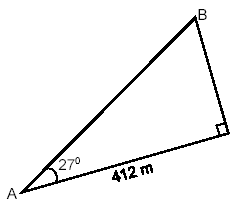
solution
We are given A = 27º and b = 412 m
To solve this triangle, we need to compute values
for B, a, and c.
When one of the acute angles is given, the
easiest way to compute the other is by
subtraction from 90º:
A + B = 90º (for a right triangle)
So, 27º + B = 90º giving B = 90º - 27º = 63º.
Then, for side a, we have
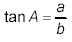or
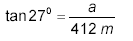which gives a = (412 m)(tan 27º)
≈ 209.92 m.
Finally, for side c,
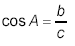or
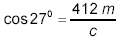giving
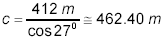
Thus, the required solution is: B = 63º, a
≈ 209.92 m, c ≈ 462.40 m
Note the strategy employed in the previous example. To calculate ‘a’, we looked for a
trigonometric ratio that involved A and b (our given quantities) and ‘a’ (the unknown we wished to
determine). Similarly, to determine c, we looked for a trigonometric ratio involving A, b, and c. In
both of these cases this meant that the definition of the selected trigonometric ratio would amount
to an equation with one unknown, which
was then easily solved.
Example 2
Solve the right triangle
shown in the figure below.
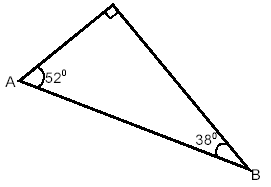
solution
The solution here is that there is no
solution. Knowing all three angles of a
right triangle is not enough information to
be able to calculate the lengths of any of
the three sides. In fact, there is an infinite
number of right triangles that have these
three angles – each of a different size.
So, we cannot obtain a unique solution for this triangle.
Example 3
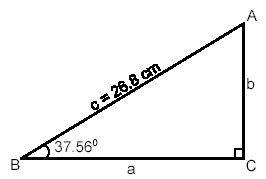
Solve the right triangle with c = 26.8 cm and B = 37.56º.
solution
| It is probably best to start by making a
sketch, as is done to the right.
In addition to the right angle, of course, the
known parts of the triangle, B and c, are
given in the statement of the problem. So,
we need to determine the values of A, a,
and b.
First, A + B = 90º so A + 37.56º = 90º giving A = 90º -
37.56º =52.44º Then,
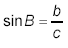gives
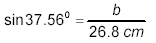or
b = (26.8 cm)(sin 37.56º)
≈ 16.34 cm
Finally, using
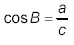or
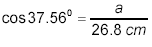gives us
a = (26.8 cm)(cos 37.56º)
≈ 21.24 cm
Thus, the required solution is
A = 52.44º, a
≈ 21.24 cm, b ≈ 16.34
cm. |
 |
|
