Equations Involving Fractions or Decimals
When a system of equations involves fractions or decimals, we can use the
multiplication property of equality to eliminate the fractions or decimals.
Example 1
A system with fractions
Solve the system:
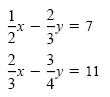
Solution
Multiply the first equation by 6 and the second equation by 12:
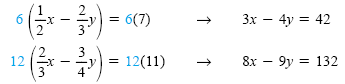
To eliminate x, multiply the first equation by -8 and the second by 3:
| -8(3x - 4y) |
= -8(42) |
→ |
-24x |
+ |
32y = |
-336 |
| 3(8x - 9y) |
= 3(132) |
→ |
24x |
- |
27y = |
396 |
| |
|
|
|
|
5y = |
60 |
| |
|
|
|
|
y = |
12 |
Substitute y = 12 into the first of the original equations:
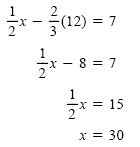
Check (30, 12) in the original system. The solution set is {(30, 12)}.
The strategy for solving a system by addition is summarized as follows.
The Addition Method
1. Write both equations in the same form (usually Ax � By � C).
2. Multiply one or both of the equations by appropriate numbers (if necessary)
so that one of the variables will be eliminated by addition.
3. Add the equations to get an equation in one variable.
4. Solve the equation in one variable.
5. Substitute the value obtained for one variable into one of the original equations
to obtain the value of the other variable.
6. Check the two values in both of the original equations.
|