Percent of Change
Objective Learn how to compute the percent of
change of a certain quantity.
When a certain quantity changes, it is often important to know
by what percent it changed. For example, the statement there was
an inflation of 5% in housing prices in the last year, means that
the cost of housing went up 5% during the year. In this lesson
you will learn how to compute the percent of change.
Computing Percent of Change
There are two methods you should learn. Have a look at the
following examples.
Example 1
Find the percent of change from 125 to 175.
Solution
Method 1 Find the difference of the
quantities (the change) and compute what percent of the original
quantity the difference is.
In this example, the difference of the quantities is 175 - 125
= 50. So the quantity increased by 50. We then need to find out
what percent the difference 50 is of the original quantity 125.
Let x represent this percent.
50 is x % of 125
Substitute a multiplication sign for the word of, we have the
equation 50 = x % · 125. Solve this equation for x. 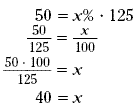
So the percent change from 125 to 175 is 40%. Since the
quantity increased from 125 to 175, we say that the percent
increase is 40%.
Method 2 When you are asking for the percent
change from 125 to 175, you are essentially asking what percent
of 125 is 175. Let y represent this percent.
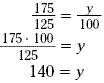
This says that 175 is 140% of 125. Since 100% of a number is
equal to that number, the percent increase is 40%.
Notice that a shortcut to this calculation is simply to divide
the new amount by the original amount.
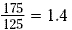
Then subtract 1 and express the resulting decimal as a
percent.
1.4 - 1 = 0.4
0.4 = 40%
|