Linear Equations and Inequalities in One Variable
PROPERTIES
| English Words |
Math Symbols |
| ⇒ COMMUTATIVE
(2 - moved) |
2 + 3 = 3 + 2
2 · 3 = 3 · 2
|
| ⇒ ASSOCIATIVE
(3 - grouped) |
(2 + 3) + 5 = 2 + (3 + 5)
(2 · 3) · 5 = 2 · (3 · 5) |
| ⇒ DISTRIBUTIVE
(multiplication over sum) |
2 (3 + 5) = 2 · 3 + 2 · 5 |
| ⇒ IDENTITY
(result = original)
|
2 + (0) = 2
3 · (1) = 3 |
| ⇒ INVERSE
(result = identity element) |
2 + (- 2) = 0
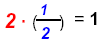 |
Rule of Thumb for signed numbers:
Remember that the sign goes with the number that follows it.
Simplifying Expressions
Definition: Two or more terms with the same variable part are called Similar
(or Liike) Terms.
Example 1:
Similar (or Liike) Terms:
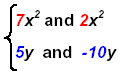
Example 2:
Simplify each expression (Combine Liike Terms):
a) 7x2 - 2x2
| 7x2 - 2x2 |
= (7 - 2)x2 |
Distributive property |
| |
= 5x2 |
Addition |
b) 5y + 3x – 10y + 8x
| 5y + 3x – 10y + 8x |
= 5y – 10y + 3x + 8x |
Commutative property |
| |
= (5y – 10y) + (3x + 8x) |
Associative property |
| |
= (5 – 10)y + (3 + 8)x |
Distributive property |
| |
= - 5y + 11x |
Addition:
|
Note: These terms cannot be combined because x ≠ y and the terms are
not like or not similar.
Since there are fewer terms in the result than the beginning expression
the result is simpler.
Example:
Apply the associative property to rewrite each of the following expressions,
and then simplify when possible.
| 1. (5x + 3) + 4 |
= 5x + (3 + 4) |
Associative Property |
| |
= 5x + 7 |
Addition |
| 2. 7+ (4 + y) |
= (7 + 4) + y |
Associative Property |
| |
= 11 + y |
Addition |
The most often missed property is the distributive property. When there is a number or
variable multiplied times an expression in parentheses, you must always make sure to
multiply times each term inside the parentheses and stop with the "close paren".
Remember that the sign goes with the number that follows it.
|