Solving Linear Inequalities in One Variable

Examples

Example 1:

Solve 6x − 3 < 2x + 5

1) Add opps: Complete the step: Then		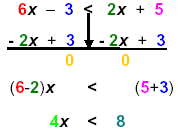Now (6-2) = 4 and (5+3) = 8 4 is the coefficient of x
2) Multiply recip: Then:		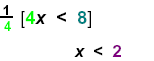Since 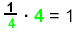and

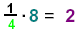 Note that 1 < 2 so use x = 1 as a replacement for x to check your answer.

Check:   or

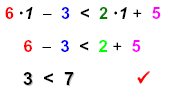Replace x with 1 and simplify.   x < 2 is correct.

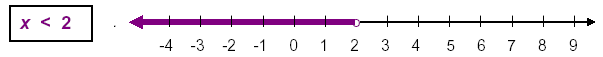
Always substitute a number in the result for x in the original inequation and check to see if that makes a “true statement”. Then you know that your result is the solution set or “answer” to the inequality.

[NOTE: For inequations there are many solutions in the solution set.]

We chose x = 1 as a replacement value to check the algebraic inequality, but we could have chosen any value on the REAL number line to the left of 2 even x = 1.999999999 which is less than 2.

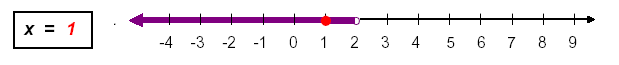
Since we can represent any REAL number on the number line we can represent ALL of the numbers that can be chosen as a replacement for the variable by shading or drawing a bold line with an arrow pointing in the direction of all other real numbers. Since x ≠ 2 we left a hole at that spot on the number line.

You should always sketch the solution to inequalities on the number line as an aid to choosing replacement values.

There are times when we want to know all of the values that are “at most 2” . From the table at the beginning of this session we see that the symbol for “at most” is ≤ which is a compound symbol.

This is really two problems in one: an equation and inequality which has the same point on the number line as a boundary. In the first case 2 is a replacement value for x and in the second case the numbers up to, but not including, 2 are replacement values. To show both cases on the number line we “fill in the hole” or put a large “dot” on that spot to represent that 2 also belongs to the replacement set.

Similarly, we can find the “solutions” or replacement values for “at least 5” which we see can be represented by the symbol ≥ and can be shown on the number line by a bold arrow pointing to the right and a “dot” to fill in the hole.
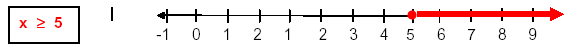