The Pythagorean Theorem
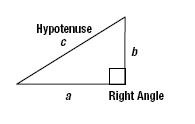
A 90° angle is a right angle, so a triangle that contains a 90° angle is
called a right triangle. The side opposite the right angle is the
hypotenuse of the triangle.
Let a and b represent the lengths of the sides that form the right angle. Let
c represent the length of the hypotenuse.
The Pythagorean Theorem states the relationship between the lengths of
the sides of a right triangle.
Formula —
Pythagorean Theorem
If a and b are the lengths of the sides that form the right angle in a
right triangle and c is the length of the hypoteneuse, then:
c2 = a2 + b2
If we know the lengths of two sides of a right triangle, we can use the
Pythagorean Theorem to find the length of the third side.
Example 1
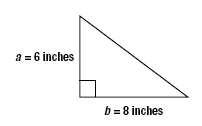
Given a right triangle with sides of length 6 inches and 8 inches, find the
length of the hypotenuse.
| Solution
In the Pythagorean Theorem, substitute
6 inches for a and 8 inches for b.
|
c2 c2 |
= a2
+ b2
= (6 inches)2 + (8 inches)2
|
|
Calculate the squares.
Add.
The value of c2 is 100.
|
|
= 36 inches2
+ 64 inches2
= 100 inches2 |
|
To find the value of c we ask,
“What positive number squared is 100?â€
That is, “What is the square root of 100?â€
The square root of 100 is 10. |
c
c |
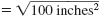
= 10 inches |
Therefore, the length of the hypotenuse, c, is 10 inches.
Example 2
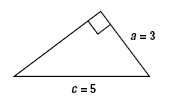
Given a right triangle where one leg has length 3 units and the hypotenuse
has length 5 units, find the length of the third side.
| Solution
In the Pythagorean Theorem, substitute 3
for a and 5 for
c.
|
c2
52 |
= a2
+ b2
= (3)2 +
b2 |
|
Calculate the squares.
Subtract 9 from both sides. |
25
16 |
=
9
+ b2 =
b2 |
|
We found that b2 is 16.
The square root of 16 is 4. |
4 |
= b |
Therefore, the length of the third side, b, is 4 units.
|