Systems of Equations
Elimination Using Addition and Subtraction
In systems of equations where the coefficients of terms
containing the same variable are opposites, the elimination
method can be applied by adding the equations. If the
coefficients of those terms are the same, the elimination method
can be applied by subtracting the equations.
Example
Solve the following system of equations using elimination.
x - 2y = 13 and 3x + 2y = 15
Solution
Add the two equations, since the coefficients of the y-terms,
-2 and 2, are opposites.
| x - 2y = 13 |
|
|
| (+) 3x + 2y = 15 |
|
|
| 4x = 28 |
|
Solve for x. |
| x = 7 |
|
|
| x - 2y = 13 |
|
Use the first equation. |
| 7 - 2y = 13 |
|
Substitute 7 for x. |
- 2y = 6 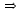 y = -3 y = -3
|
The solution of the system is (7, - 3).
Elimination Using Multiplication
An extension of the elimination method is to multiply one or
both of the equations in a system by some number so that adding
or subtracting eliminates a variable.
Example
Solve the following system of equations using elimination.
x - y = 5 and 3x + 2y = 15
Solution
Multiply the first equation by 2 so that the coefficient of
the y-terms in the system will be opposites. Then, add the
equations and solve for x.
| 2(x - y) = 2(5) |
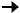 |
2x - 2y = 10 |
| 3x + 2y = 15 |
(+) 3x + 2y = 15 |
| |
|
5x = 25 |
| |
|
x = 5 |
| x - y = 5 |
|
Use the first equation. |
| 5 - y = 5 |
|
Substitute 5 for x. |
-y = 0 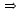 y = 0 y = 0 |
The solution to this system is (5, 0).
|