Laws of Exponents and Multiplying Monomials

Objective Learn the algebra of polynomials by using the laws of exponents to multiply and divide monomials.

The main ideas in this lesson are the laws for multiplying and dividing powers. In this lesson, we will deal with monomials that are powers of a single variable.

Powers

Let's begin by reviewing powers and exponents. If a is a variable, then a ² represents a · a , a ³ represents a · a · a , and more generally, a ^b represents

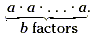
Remember that a is called the base, b is called the exponent, and a ^b is called the power. Also, the power a ⁴ is read "a raised to the fourth power". In general, when we write a ^b, we say "a raised to the b power".

When multiplying monomials, we must analyze the product of the two powers of the same base. Consider x ² · x ³. Let' s analyze this by multiplying various powers of 2 together.

2 ² · 2 ³ = 4 · 8 = 32 = 2 ⁵

2 ⁴ · 2 ⁵ = 16 · 32 = 512 = 2 ⁹

In both cases, the exponent of the resulting power is the sum of the exponents in the two factors. For 2 ² · 2 ³ , 5 = 2 + 3, and for 2 ⁴ · 2 ⁵ ,9 = 4 + 5. The table shows what happens when a power of 2 is multiplied by "2 to the first power," which is 2. Recall that any number raised to the first power is the number itself.

Notice each power that results. Do you see a pattern? Each resulting power can be found by adding 1 to the exponent of the original power. For example, 2 ³ · 2 ¹ = 2 ^{3 + 1} or 2 ⁴ . Using symbols, we write 2 ⁿ · 2 ¹ = 2 ^{n + 1}. The following table shows what happens when a power of 2 is multiplied by "2 to the second power" or 4.

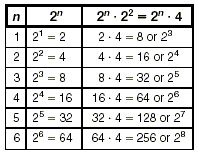
Again, notice each power that results. In this case, each power can be found by adding 2 to the exponent of the original power. For example, 2 ³ · 2 ² = 2 ^{3 + 2} or 2 ⁵. Using symbols, we write 2 ⁿ · 2 ² = 2 ^{n + 2}.

This confirms our earlier observation that when we multiply two powers that have the same base, the exponent of the resulting power is the sum of the exponents in the two factors.

Now is a good time to explore this idea for yourself. Choose your own bases and exponents. Then evaluate both a ^b · a ^c and a ^{b + c} to verify that they are equal. Why is this true? Remember th at exponents area shorthand that represents a repeated product of the same number or variable. So,

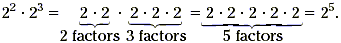
In general, when we multiply a ^b and a ^c, we'll get

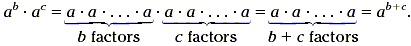
Key Idea

When we multiply a power of a times another power of a, the result is a power of a , where the exponent is the sum of the exponents of the two factors. In symbols,

a ^b · a ^c = a ^{b + c}

This holds true for any number a and positive integers b and c .