Solving Quadratic Equations by Completing the Square
Example 1
Completing the square with a = 1
Solve x2 + 6x + 5 = 0 by completing the square.
Solution
The perfect square trinomial whose first two terms are x2 + 6x is
x2 + 6x + 9.
So we move 5 to the right-hand side of the equation, then add 9 to each side:
| |
= -5 |
Subtract 5 from each side. |
| |
= -5 + 9 |
Add 9 to each side to get
a perfect square trinomial. |
| |
= 4 |
Factor the left-hand side. |
| |
= ±
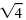 |
Even-root property |
| x + 3 |
= 2 |
or |
x + 3 |
= -2 |
|
| x |
= -1 |
or |
x |
= -5 |
|
Check in the original equation:
(-1)2 + 6(-1) + 5 = 0 and
(-5)2 + 6(-5) + 5 = 0
The solution set is {-1, -5}.
Caution
The perfect square trinomial that we have used so far
had a leading coefficient of 1. If a ≠ 1, then we must divide each side of the equation
by a to get an equation with a leading coefficient of 1.
The strategy for solving a quadratic equation by completing the square is stated
below.
Strategy for Solving Quadratic Equations
by Completing the Square
1. The coefficient of x2 must be 1.
2. Get only the x2 and the x terms on the left-hand side.
3. Add to each side the square of
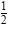 the coefficient of x. the coefficient of x.
4. Factor the left-hand side as the square of a binomial.
5. Apply the even-root property.
6. Solve for x.
7. Simplify.
In our procedure for completing the square the coefficient of x2 must be 1.
We can solve ax2 + bx + c = 0 with a ≠ 1 by completing the square if we first
divide each side of the equation by a.
|