Invariants Under Rotation
Have a look at the following theorem:
THEOREM 1
Rotation of Axes
The general equation of the conic
Ax2 + Bxy + Cy2 + Dx + Ey + F = 0
where B ≠ 0, can be rewritten as
A'(x')2 + B'x'y' + C'(y')2 + D'x' + E'y' + F' = 0
by rotating the coordinate axes through an angle
θ, where
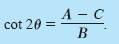
Note that the constant term is the same in both equations.
Because of this, F is said to be invariant under rotation. The following
theorem lists some
other rotation invariants. The proof of this theorem is left as an exercise.
Theorem 2
Rotation Invariants
The rotation of coordinate axes through an angle
θ that transforms the equation Ax2 + Bxy + Cy2 + Dx + Ey + F = 0
into the form
A'(x')2 + B'x'y' + C'(y')2 + D'x' + E'y' + F' = 0
has the following rotation invariants.
1. F = F'
2. A + C = A' + C'
3. B2 - 4AC = (B')2 - 4A'C'
You can use this theorem to classify the graph of a second-degree equation with
an xy-term in much the same way you do for a second-degree equation without an xy-term.
Note that because B' = 0, the invariant B2 - 4AC reduces to
| B2 - 4AC = - 4A'C' |
Discriminant |
which is called the discriminant of the equation
Ax2 + Bxy + Cy2 + Dx + Ey + F = 0
Because the sign of A'C' determines the type of graph for the equation
A'(x')2 + B'x'y' + C'(y')2 + D'x' + E'y' + F' = 0
the sign of B2 - 4AC must determine the type of graph for the original equation. This
result is stated in the following theorem.
Theorem 3
Classification of Conics by the Discriminant
Ax2 + Bxy + Cy2 + Dx + Ey + F = 0
is, except in degenerate cases, determined by its discriminant as follows.
| 1. Ellipse or circle |
B2 - 4AC < 0 |
| 2. Parabola |
B2 - 4AC = 0 |
| 3. Hyperbola |
B2 - 4AC > 0 |
Example
Using the Discriminant
Classify the graph of each of the following equations.
a. 4xy - 9 = 0
b. 2x2 - 3xy + 2y2 - 2x = 0
c. x2 - 6xy + 9y2 - 2y + 1 = 0
d. 3x2 + 8xy + 4y2 - 7 = 0
Solution
a. The graph is a hyperbola because
B2 - 4AC = 16 - 0 > 0.
b. The graph is a circle or an ellipse because
B2 - 4AC = 9 - 16 < 0.
c. The graph is a parabola because
B2 - 4AC = 36 - 36 = 0
d. The graph is a hyperbola because
B2 - 4AC = 64 - 48 > 0
|