Roots
For even values of n , the expression 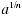 is defined
to be the positive nth root of a or the principal nth root of a.
For example, is defined
to be the positive nth root of a or the principal nth root of a.
For example, 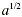 denotes the positive second root, or square root, of
a , while denotes the positive second root, or square root, of
a , while 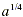 is the positive fourth root of a. When n is odd,
there is only one n th root, which has the same sign as a. For
example, is the positive fourth root of a. When n is odd,
there is only one n th root, which has the same sign as a. For
example, 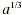 ,
the cube root of a, has the same sign as a. By definition, if ,
the cube root of a, has the same sign as a. By definition, if 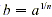 then then 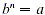 . On a
calculator, a number is raised to a power using a key labeled . On a
calculator, a number is raised to a power using a key labeled 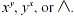 For example,
to take the fourth root of 6 on a TI-83 calculator, enter For example,
to take the fourth root of 6 on a TI-83 calculator, enter 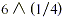 , to get the
result 1.56508458. , to get the
result 1.56508458.
EXAMPLE 1
Calculations with Exponents
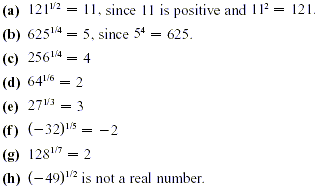
Rational Exponents
In the following definition, the domain of an exponent is
extended to include all rational numbers.
DEFINITION OF 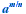
For all real numbers a for which the indicated roots exist,
and for any rational number m/n
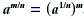
EXAMPLE 2
Calculations with Exponents
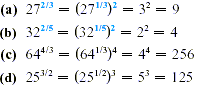
NOTE 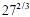 could also be evaluated as could also be evaluated as 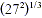 but this is
more difficult to perform without a calculator because it
involves squaring 27, and then taking thecube root of this large
number. On the other hand, when we evaluate it as but this is
more difficult to perform without a calculator because it
involves squaring 27, and then taking thecube root of this large
number. On the other hand, when we evaluate it as 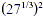 we know that
the cube root of 27 is 3 without using a calculator, and squaring
3 is easy. we know that
the cube root of 27 is 3 without using a calculator, and squaring
3 is easy.
All the properties for integer exponents given in this section
also apply to any rational exponent on a nonnegative real-number
base.
EXAMPLE 3
Simplifying Exponential Expressions
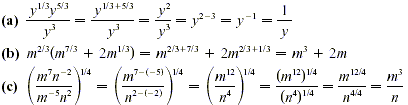
In calculus, it is often necessary to factor expressions
involving fractional exponents.
EXAMPLE 4
Simplifying Exponential Expressions
Factor out the smallest power of the variable, assuming all
variables represent positive real numbers.
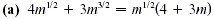
Solution
To check this result, multiply by 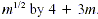
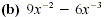
Solution
The smallest exponent here is 3. Since 3 is a common numerical
factor, factor out 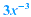 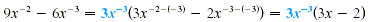
Check by multiplying. The factored form can be written without
negative exponents as
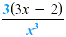 . .
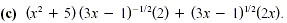
Solution
There is a common factor of 2. Also, 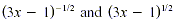 have a
common factor. Always factor out the quantity to the smallest
exponent. Here -1/2 < 1/2 so the common factor is have a
common factor. Always factor out the quantity to the smallest
exponent. Here -1/2 < 1/2 so the common factor is 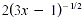 and the
factored form is and the
factored form is
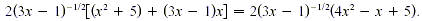
|