Simplifying Radicals Involving Variables
Examples
In the following example we start with a square root of a quotient.
Example 1
Radicals with variables
Simplify each expression. Assume all variables represent positive real numbers.
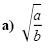
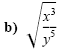
Solution
 |
 |
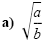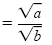Quotient rule for radicals |
| |
 |
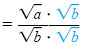Rationalize the denominator. |
| |
 |
|
 |
 |
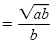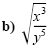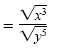Quotient rule for radicals |
| |
 |
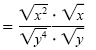Product rule for radicals |
| |
 |
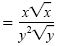Simplify. |
| |
 |
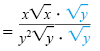Rationalize the denominator. |
| |
 |
|
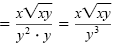Any variable with an exponent that is a multiple of 3 is a perfect cube.
For example, a3, b6, c15, and w39
are perfect cubes. Each of these expressions is the cube of a variable with an
integral exponent. For any values of the variables we can write
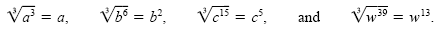
Note that when we find the cube root, the result has one-third of the
original exponent.
If the exponent on a variable is a multiple of 4, we have a perfect fourth
power; if the exponent is a multiple of 5, we have a perfect fifth power; and so
on. In the next example we simplify radicals with an index higher than 2.
Example 2
Simplifying higher-index radicals with variables
Simplify. Assume the variables represent positive numbers.
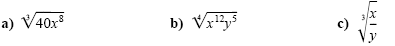
Solution
a) Use the product rule to place the largest perfect cube factors under the
first radical and the remaining factors under the second:
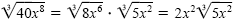
b) Place the largest perfect fourth power factors under the first radical and
the remaining factors under the second:
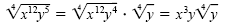
c) Multiply by
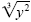 to
rationalize the denominator:
|
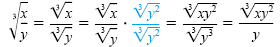
