Inequalities
As with an equation, we solve an inequality in the variable X
by finding all values of X for which the inequality is true. Such
values are called solutions and we say that the solutions satisfy
the inequality. The set of all real numbers that are solutions of
an inequality is called the solution set of the inequality. The
procedures for solving linear inequalities in one variable are
much like those for solving linear equations. To isolate the
variable we make use of properties of inequalities which are
similar to the properties of equality. However, there is an
important exception. WHEN BOTH SIDES OF AN INEQUALITY ARE
MULTIPLIED OR DIVIDED BY A NEGATIVE NUMBER, THE DIRECTION OF THE
INEQUALITY SYMBOL MUST BE REVERSED. Solve the linear inequality
and sketch the solution set on the real number line.
Example
Solve the linear inequality and sketch the solution set on the
real number line.
Solution
A.
2X + 3 > 4
2X > 1
X > 1/2
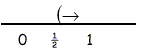
B.
3X - 4 < 2x - 5
x < 9
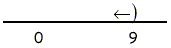
C.
- 5X + 4 > 3
- 5X > -1
X < 1/5
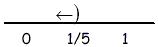
To solve a quadratic inequality, we use the fact that a
polynomial can change signs only at its zeros (the x-values that
make the polynomial zero). Between two consecutive zeros a
polynomial must be entirely positive or entirely negative. This
means that when the real zeros of a polynomial are put in order,
they divide the real line into intervals in which the polynomial
has no sign changes. We call these zeros the critical numbers of
the inequality and we call the resulting intervals the test
intervals for the inequality. To determine the intervals on which
the values of a polynomial are entirely negative or entirely
positive, use the following steps.
1. Find all the real zeros of the polynomial, and arrange the
zeros in increasing order (from smallest to largest). The zeros
of the polynomial are its critical numbers.
2. Use the critical numbers of the polynomial to determine its
test intervals.
3. Choose one representative x-value in each test interval and
evaluate the polynomial at that value. If the value of the
polynomial is negative, then the polynomial will have negative
values for every x-value in that interval. If the value of the
polynomial is positive, then the polynomial will have positive
values for every x-value in that interval.
The concepts of critical numbers and test intervals can be
extended to inequalities involving rational expressions. To do
this, we use the fact that the value of a rational expression can
change signs only at its zeros (the x-value for which its
numerator is zero) and its undefined values (the xvalues for
which its denominator is zero). These two types of numbers make
up the critical numbers of a rational inequality.
|