Polar Form of a Complex Number

Just as real numbers can be represented by points on the real number line, you can represent a complex number z = a + bi at the point (a, b) in a coordinate plane (the complex plane). The horizontal axis is called the real axis and the vertical axis is called the imaginary axis, as shown in the figure below.

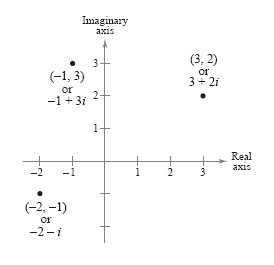
The absolute value of the complex number a + bi is defined as the distance between the origin (0, 0) and the point (a, b).

The Absolute Value of a Complex Number

The absolute value of the complex number z = a + bi is given by

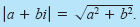
NOTE

If the complex number a + bi is a real number (that is, if b = 0), then this definition agrees with that given for the absolute value of a real number.

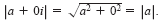
To work effectively with powers and roots of complex numbers, it is helpful to write complex numbers in polar form. In the figure below, consider the nonzero complex number a + bi.

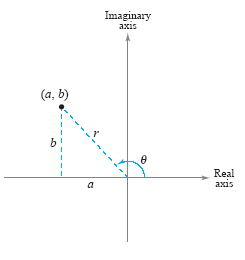
By letting θ be the angle from the positive x-axis (measured counterclockwise) to the line segment connecting the origin and the point (a, b), you can write a = cos θ and b = r sin θ where 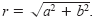Consequently, you have

a + bi = (r cos θ) + (r sin θ)i

from which you can obtain the polar form of a complex number.

Polar Form of a Complex Number

The polar form of the complex number z = a + bi is

z = r (cos θ + i sin θ)

where a = r cos θ, b = r sin θ, 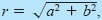and tan θ = b/a. The number r is the modulus of z, and θ is called an argument of z.

NOTE

The polar form of a complex number is also called the trigonometric form. Because there are infinitely many choices for θ, the polar form of a complex number is not unique. Normally, θ is restricted to the interval 0 ≤ θ < 2π, although on occasion it is convenient to use θ < 0.