Exponential Growth: Compound Interest

An example of an exponential growth function is compound interest. Compound interest means that the interest you earn after a certain period of time is added to your initial investment. Then, you earn interest on your initial investment and on the interest that you have earned. That is, your interest compounds.

The following formula can be used to calculate compound interest.

Formula — Compound Interest With n Compounding Periods

The amount of money in an account that earns compound interest is given by the following formula:

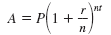
where:

A = amount in the account after t years.

P = principal (amount on which the interest is calculated).

r = annual percentage rate, written in decimal form.

n = number of times the interest is compounded per year.

t = number of years the money is invested.

Example 1

Wendy invested $1000 in an account that earns 6% interest per year.

a. Find the amount, A, after 5 years if the interest is compounded quarterly.

b. Use the graph to approximate the number of years it will take for the investment to be worth $2000.

Solution

a.	Use the compound interest formula. Amount invested, P = 1000. Interest rate, r = 6% = 0.06. Number of times compounded per year, n = 4 Number of years invested, t = 5.
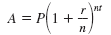	Substitute the values for the variables.
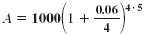	Simplify inside the parentheses. Simplify the exponent. Use a calculator to find (1.015)20. Leave the result on your calculator until you multiply by 1000. This will minimize the rounding error. Multiply and round to the nearest cent. Multiply and round to the nearest cent.	A = 1000(1.015)4 · 5 A = 1000(1.015) 20     A ≈ 1000 (1.346855007) A ≈ $ 1346.86
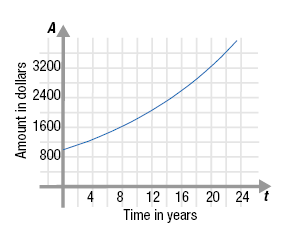
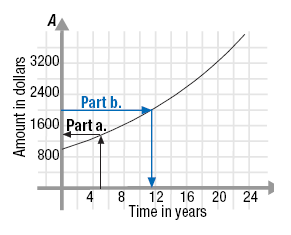
	So, after 5 years Wendy will have approximately $1346.86. We can use the graph to check that $ 1346.86 is a reasonable solution. • First, find t = 5 on the t-axis. • Then, move vertically until you intersect the graph. • Then move left to the A-axis. • Finally read the value. The value appears to be about $ 1400. So, our calculation of $1346.86 is reasonable.
b.	On the graph, find 2000 on the A-axis. Then, move horizontally until you intersect the graph, move down to the t-axis, and finally read the value. It appears to be slightly less than 12, say 11.6. So, the amount in the account will grow to $2000 in about 11.6 years.

Note:

To find 1.015²⁰ on a scientific calculator, enter 1.015, then press the key, then enter 20, then press the key.

A typical calculator displays a maximum of ten digits. Therefore, we will initially show ten digits in our calculations.

Because the number displayed is not exact, we use the ≈ symbol instead of =. The ≈ symbol means “approximately equal to.”