Absolute Value and Distance
If a is a real number, the absolute value of a is
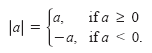
The absolute value of a number cannot be negative. For example, let a = -4. Then,
-4 < 0, because you have
| a | = | -4 | = -(-4) = 4.
Remember that the symbol -a does not necessarily mean that is -a negative.
Operations with Absolute Value
Let a and b be real numbers and let n be a positive integer.
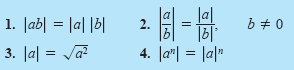
Properties of Inequalities and Absolute Value
Let a and b be real numbers and let k be a positive real number.
1. -| a | ≤ a ≤ | a |
2. | a | ≤ k if and only if -k ≤ a ≤ k.
3. k ≤ | a | if and only if k ≤ a or a ≤ -k.
4. Triangle Inequality: | a + b | ≤ | a | + | b
|
Properties 2 and 3 are also true if ≤ is
replaced by <.
Example 1
Solving an Absolute Value Inequality
Solve | x - 3| ≤ 2.
Solution
Using the second property of inequalities and absolute value, you can
rewrite the original inequality as a double inequality.
| -2 ≤ |
x - 3 |
≤ 2 |
Write as double inequality.
|
| -2 + 3 ≤ |
x - 3 + 3 |
≤ 2 + 3 |
Add 3.
|
| 1 ≤ |
x |
≤ 5 |
Simplify.
|
The solution set is [1, 5], as shown in the figure below.
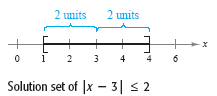
Example 2
A Two-Interval Solution Set
Solve 3 < | x + 2 |
Solution
Using the third property of inequalities and absolute value, you can rewrite
the original inequality as two linear inequalities.
| 3 < x + 2 |
or |
x + 2 < -3 |
| 1 < x |
or |
x < -5 |
The solution set is the union of the disjoint intervals (-∞,
-5) and (1, ∞) as shown in the figure
below.
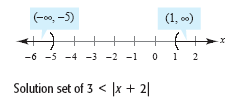
Examples 1 and 2 illustrate the general results shown in the figure below.
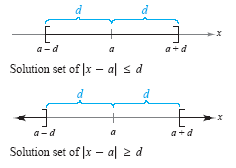
Note that if d > 0,
the solution set for the inequality | x - a | ≤
d is a single interval, whereas the
solution set for the inequality | x - a | ≥
d is the union of two disjoint intervals.
The distance between two points a and b on the real line is given by
d = | a - b | = | b - a |
The directed distance from a to b is b - a and the directed distance from b to a
is
as shown in the figure below.

Example 3
Distance on the Real Line
a. The distance between -3 and 4 is
or
| 4 - (-3)| = | 7 | = 7 or | -3 - 4 | = | -7 | =
7.
(See the figure below.)
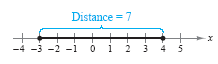
b. The directed distance from -3 to 4 is 4 - (-3) = 7.
c. The directed distance from 4 to -3 is -3 - 4 = -7.
The midpoint of an interval with endpoints a and b is the average value of a and
b. That is,

To show that this is the midpoint, you need only show that (a + b)/2 is equidistant
from a and b.
|